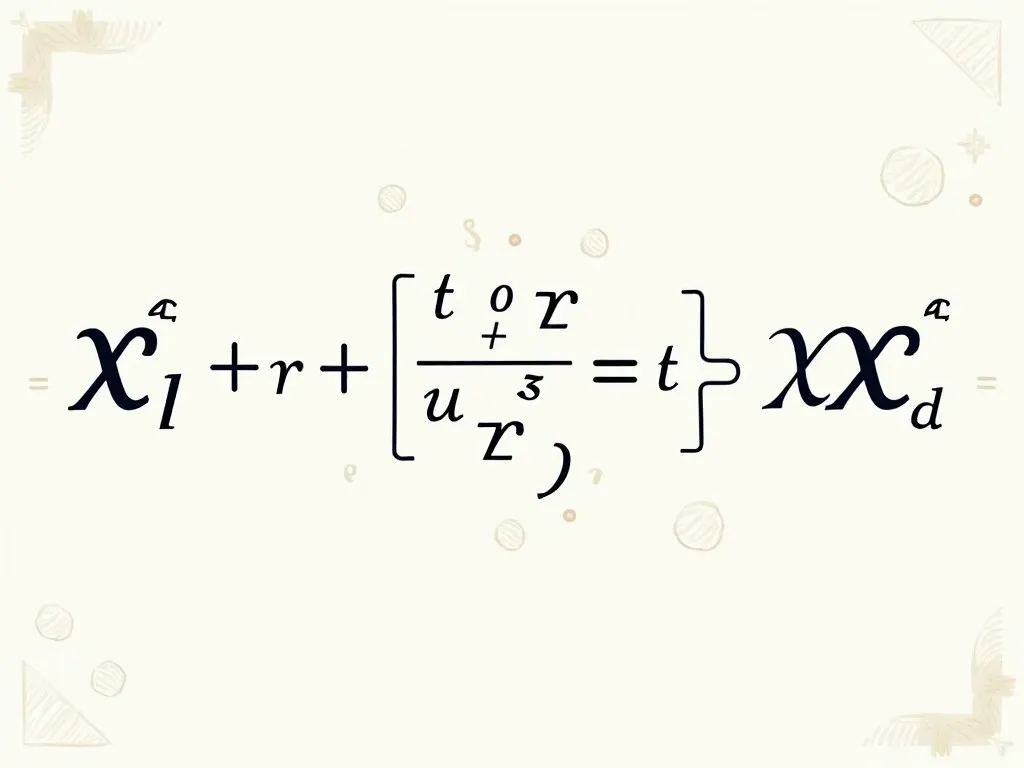球の体積を求める公式は、V = \(\dfrac{4}{3}\pi r^3\) です。この公式は、球の半径 (r) を用いて球の体積 (V) を計算するために使用されます。
球の体積の求め方
まず、公式の各要素について説明します。
- V: 球の体積
- r: 球の半径
- π: 円周率(約3.14)
球の体積を計算するためには、以下の手順を踏みます:
- 半径 (r) を測定します。
- 公式に従って、\(\dfrac{4}{3}\pi r^3\) を計算します。
計算例
例えば、半径が 3 cm の球の場合:
\[ V = \dfrac{4}{3}\pi (3)^3 = \dfrac{4}{3}\pi (27) = 36\pi \approx 113.1 \text{ cm}^3 \]
球の体積の視覚化
公式を記憶するための工夫
公式を暗記するのは大変ですが、語呂合わせを使うことで記憶しやすくなります。例えば:
「さんしろう、おいしいパイを持ってある日参上」と覚えると良いでしょう!🍰
まとめと練習問題
球の体積を求める公式 V = \(\dfrac{4}{3}\pi r^3\) は、数学や物理学において非常に重要です。以下の練習問題に挑戦してみてください!
- 半径が 5 cm の球の体積を計算してください。
- 半径が 10 cm の球の体積を計算してください。
- 半径が 1 m の球の体積を計算してください。
このページが皆さんの数学の理解を深める助けになれば幸いです。もっと学びたい方は、ぜひ他のリソースを参考にしてくださいね!📚