扇形公式 – 面積・弧の長さ・中心角の求め方

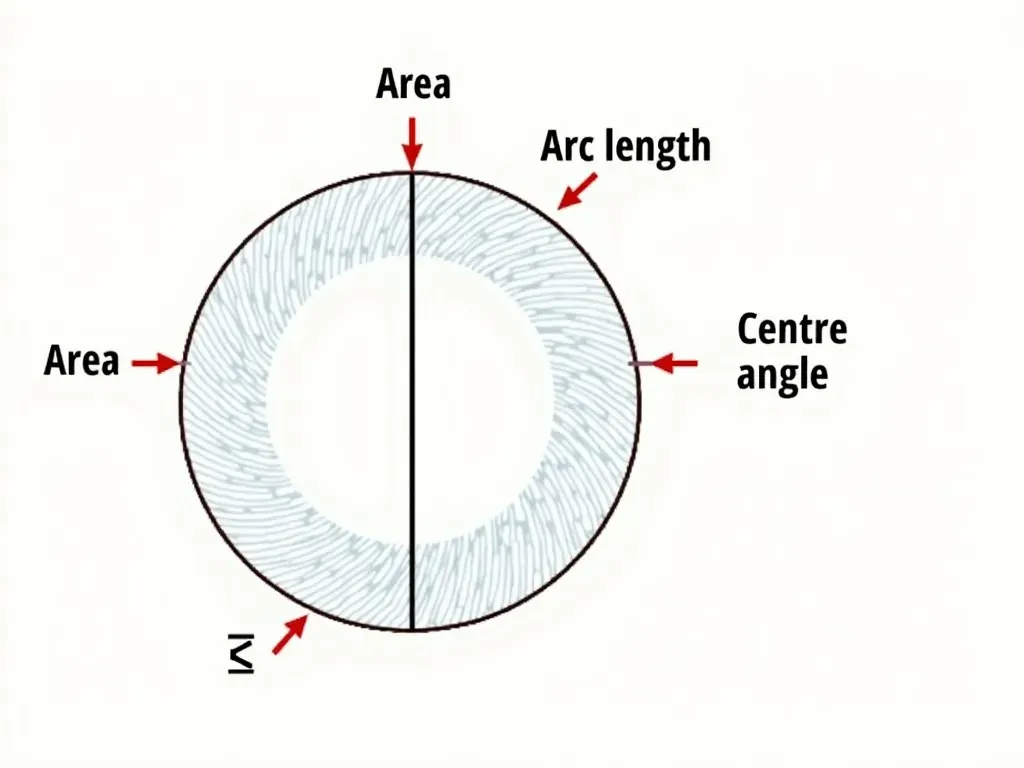
扇形（おうぎがた）とは、円の一部分であり、円の中心から放射状に伸びる2本の線と、その間の弧で構成されます。扇形の面積や弧の長さ、中心角、半径などの公式は、数学における基礎的な要素です。

扇形の面積を求める公式

扇形の面積は次の公式を使って求められます：

$$ S = \frac{\theta}{360} \times \pi r^2 $$

ここで、$S$は面積、$\theta$は中心角（度）、$r$は半径です。

例えば、半径が3 cmで中心角が90度の扇形の面積は次のように計算されます：


    S = (90/360) * π * (3^2) = 9π/4 \approx 7.07 \, \text{cm}^2

扇形の弧の長さは次の公式で求めます：

$$ L = \frac{\theta}{360} \times 2\pi r $$

ここで、$L$は弧の長さ、$r$は半径、$\theta$は中心角です。

上記の例を用いると、弧の長さは次のように計算します：


    L = (90/360) * 2 * π * 3 = 4.71 \, \text{cm}

与えられた扇形の面積から中心角を求めるための公式は次の通りです：

$$ \theta = \frac{S \times 360}{\pi r^2} $$

ここで、$S$は面積です。

扇形の面積が7.07 cm²で、半径が3 cmのとき、中心角は：


    θ = (7.07 * 360) / (π * (3^2)) \approx 90\, \text{度}