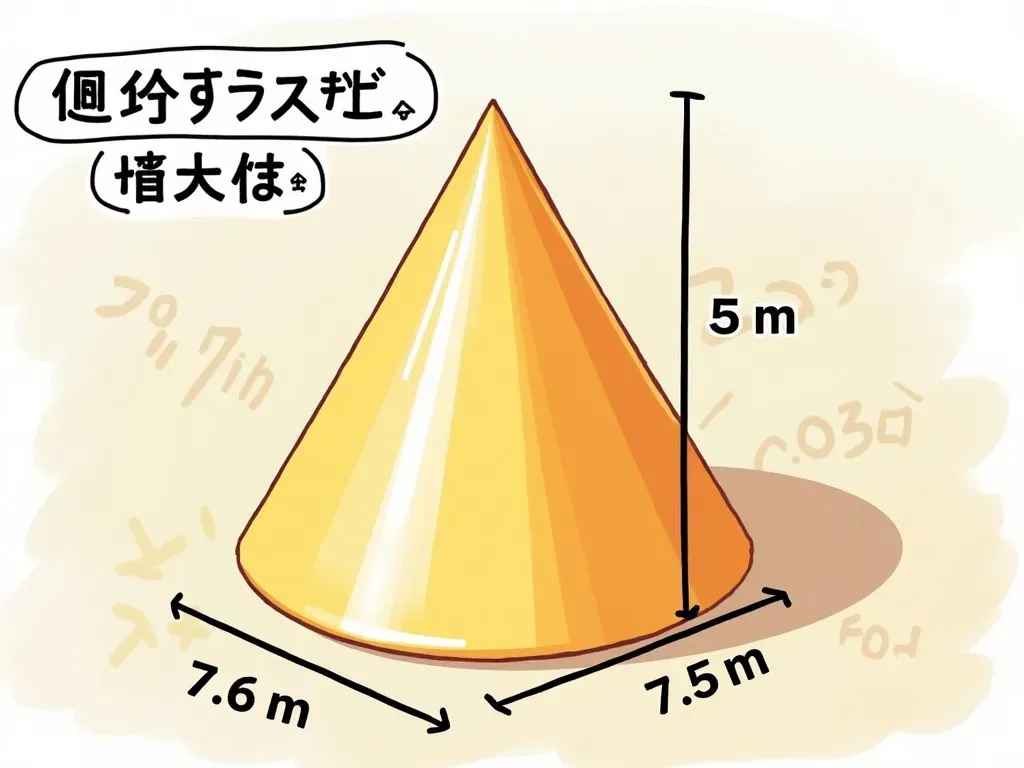
円錐の体積を求める公式は、非常にシンプルですが、実用的な場面でよく使用されます。基本的な公式は、以下のように表されます。
体積 = 底面積 × 高さ ÷ 3
これを数学的に表現すると、V = \frac{1}{3}Sh = \frac{1}{3} \pi r^2 hとなります。
円錐の定義
円錐は、底面が円で、頂点から底面に垂直にはられた線が高さとなる三次元の立体です。特に、円錐の体積を求めるためには、半径 (r) と 高さ (h) を知る必要があります。
公式の詳細
円錐の体積を求める公式は次のようになります:
V = \frac{1}{3} \pi r^2 h
ここで、rは底面の半径、hは高さです。この公式は、円柱の体積に対して、1/3を掛けることで導出されます。
計算例
では、具体的に例を使って計算してみましょう。
底面の半径が5 cm、高さが10 cmの円錐の場合:
V = \frac{1}{3} \pi (5 \: \text{cm})^2 (10 \: \text{cm})
計算すると、体積は約83.33 cm³になります。
円錐体積の用途
円錐の体積公式は、様々な実生活のシーンで活用されます。例として:
- アイスクリームのコーン 🍦の体積計算
- ドーム型建築物の設計 🏛️
- 科学実験における容器の容量
円錐のグラフィカルな表現
まとめ
円錐の体積を求める公式は非常にシンプルですが、多くの実生活の場面で役立ちます。公式をしっかりと理解し、計算を行うことで、数学に対する自信もつくでしょう!
是非、自分でもいくつかの例を使って、円錐の体積を計算してみてください。📏✏️