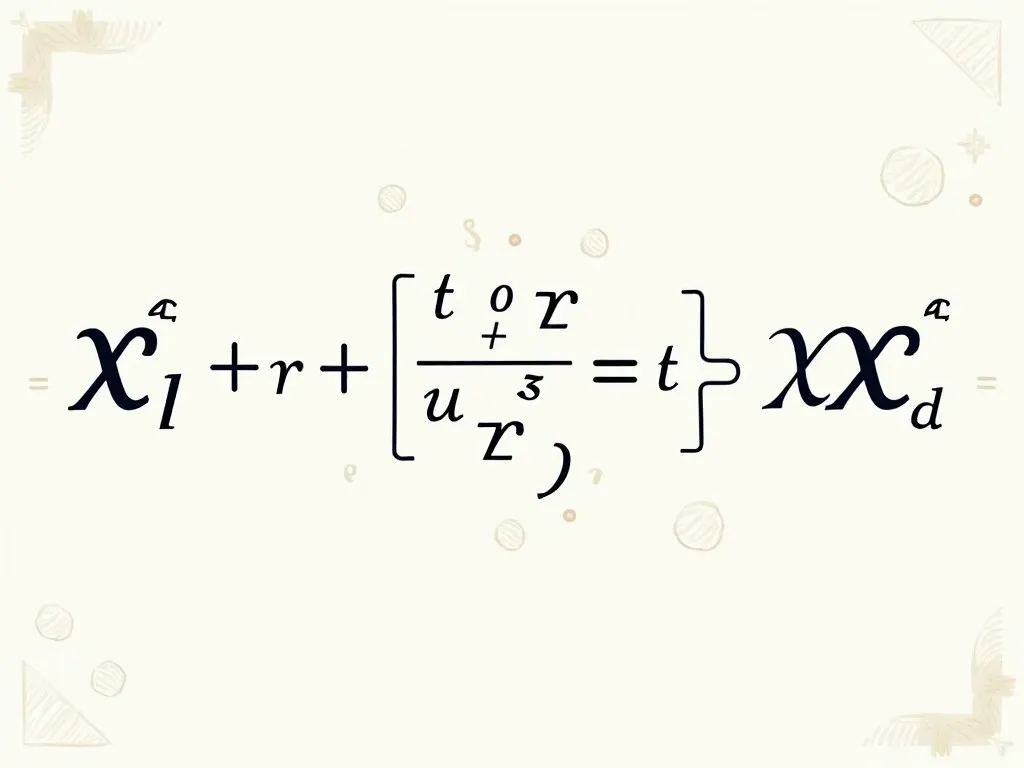数学の中で円の方程式は特に重要なトピックです。さあ、円の方程式公式の基本から応用まで、楽しく学んでいきましょう!🎉
円の方程式とは?
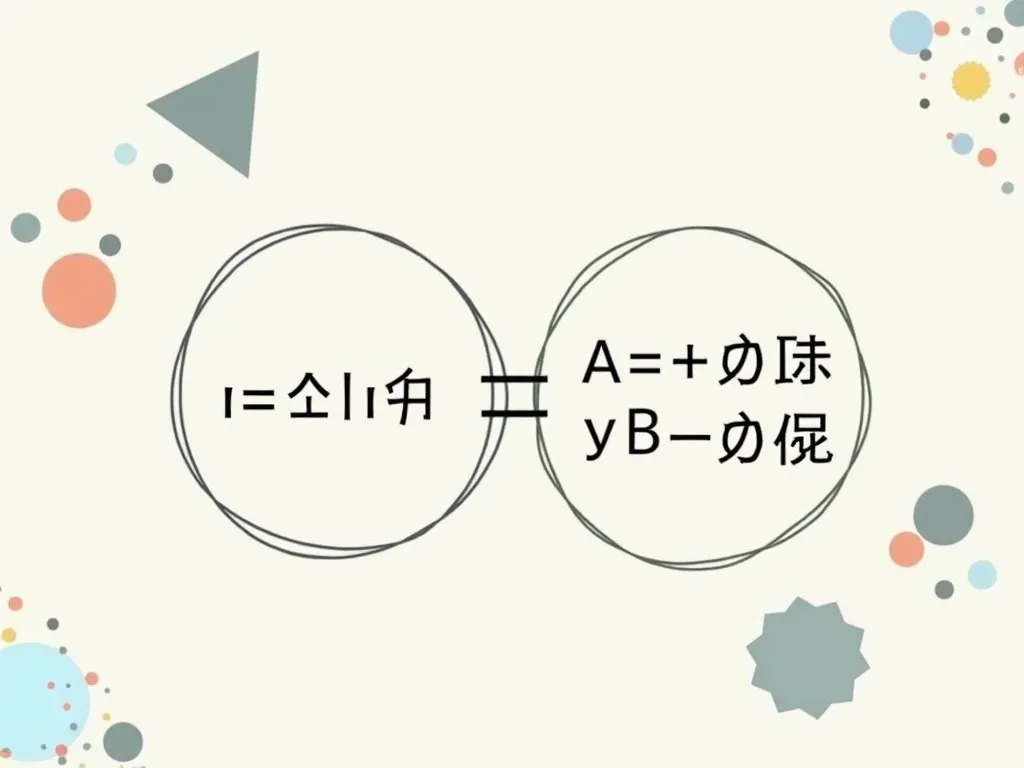
円の方程式は、円の中心 (a, b) と半径 r に基づいて定義されます。基本的な円の方程式は次の通りです:
\( (x – a)^2 + (y – b)^2 = r^2 \)
中心が原点 (0, 0) の場合、式は次のようになります:
\( x^2 + y^2 = r^2 \)
円の方程式の種類
円の方程式には主に2つの形があります:
- 基本形: \( (x – a)^2 + (y – b)^2 = r^2 \)
- 一般形: \( Ax^2 + Ay^2 + Bx + Cy + D = 0 \)
基本形について
基本形は円の中心と半径が直感的に理解できるため、数学の初学者にとっては非常に使いやすいです。
一般形について
一方、一般形は円がどのように見えるかを記述するためのものです。これを使うことで、円の接線や交点の問題を解決する手助けになります。さて、ここで公式の変換を見てみましょう。
円の方程式の求め方
円の方程式は、与えられた条件に基づいて設定できます。例えば、2点が与えられた際の方法をご紹介します。
ポイント: 与えられた2点を直径とする円の方程式を求める際は、まずその2点の中点を計算し、半径を求める必要があります。
例題を通して学ぶ
例題: 中心が(1, -2)、半径が3の円の方程式を求めよ。
解答: 与えられた情報を基本形に代入します。したがって、円の方程式は:
\( (x – 1)^2 + (y + 2)^2 = 3^2 \)
これは :
(x - 1)^2 + (y + 2)^2 = 9
円の接線について
円の接線は円に対して垂直に交差する直線です。円と接線の詳細は円の方程式の理解に欠かせません。
まとめ
円の方程式についての学習が進んだでしょう。数学は楽しみながら学ぶことが大切です。今後もこの公式を活用して、様々な問題に挑戦してみてください!💪