内接円の半径公式の詳細ガイド

私たちが数学を学ぶ中で、内接円は非常に興味深いテーマの一つです。特に、三角形の内接円の半径を求める公式は、数学のさまざまな問題で頻繁に使用されます。このページでは、公式の概要、計算方法、そして実際の例題を通して、その理解を深めていきましょう。

1. 内接円とは？
2. 内接円の半径の公式
3. 半周の計算
4. 実例を通して学ぶ ⚙️
5. グラフで視覚化する 📊
6. まとめとさらなる学び 🎓

1. 内接円とは？

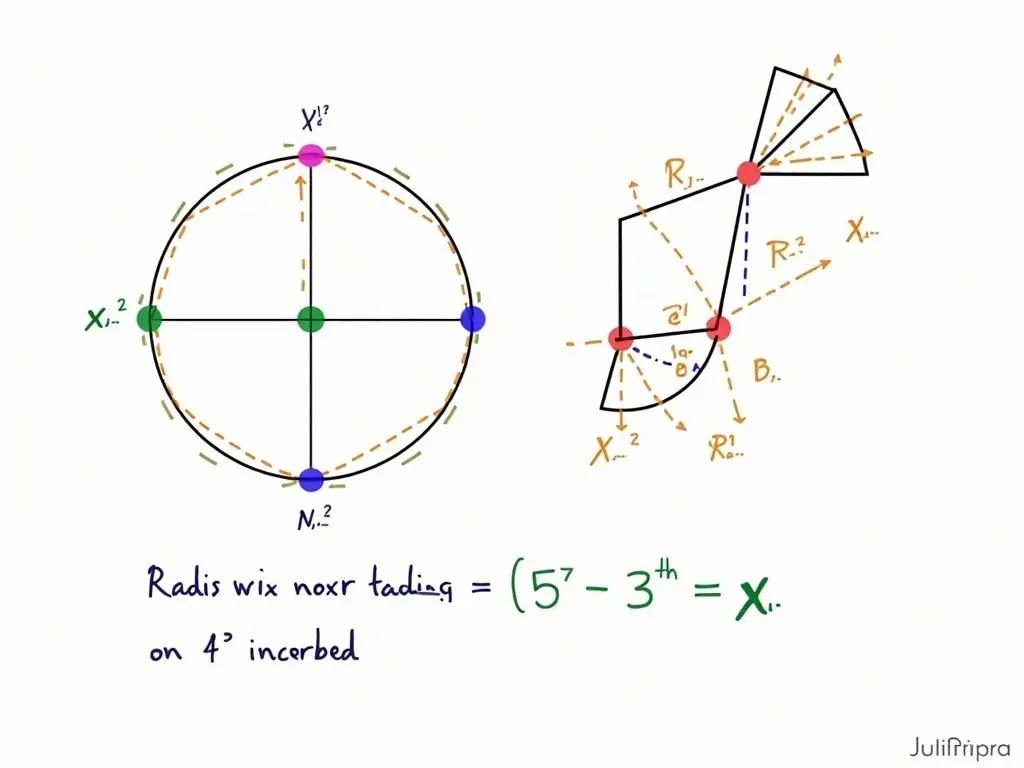
内接円とは、三角形の各辺に接する円のことです。この円の中心は、三角形の各角の二等分線が交わる点にあります。この点を内心と呼びます。

「すべての三角形には、必ず内接円が存在します。この円の半径を求めることは、幾何学の面白い挑戦の一つです。」 – 数学愛好者

2. 内接円の半径の公式

三角形の内接円の半径（r）は、次の公式を使って計算することができます：

r = \frac{S}{s}

ここで、Sは三角形の面積、sは三角形の半周（すべての辺の長さの合計の半分）です。

3. 半周の計算

半周は次のように計算されます：

s = \frac{a + b + c}{2}

ここで、a、b、cは三角形の各辺の長さです。

4. 実例を通して学ぶ ⚙️

例えば、辺の長さが a = 5, b = 6, c = 7 の三角形を考えてみましょう。

1. 半周を計算します:
   s = (5 + 6 + 7) / 2 = 9
2. ヘロンの公式を使って面積を求めます:
   S = √(s(s - a)(s - b)(s - c)) 
   = √(9(9 - 5)(9 - 6)(9 - 7)) 
   = √(9 * 4 * 3 * 2) 
   = 12
3. 内接円の半径を求めます:
   r = S / s = 12 / 9 = 4/3 約 1.33