ドップラー効果は、波動に関する非常に興味深い現象です。特に音や光の波動において、波源または観測者の動きによって観測される周波数が変化するという特徴があります。このページでは、ドップラー効果の公式、原理、実生活での応用について詳しく解説します。
ドップラー効果とは?
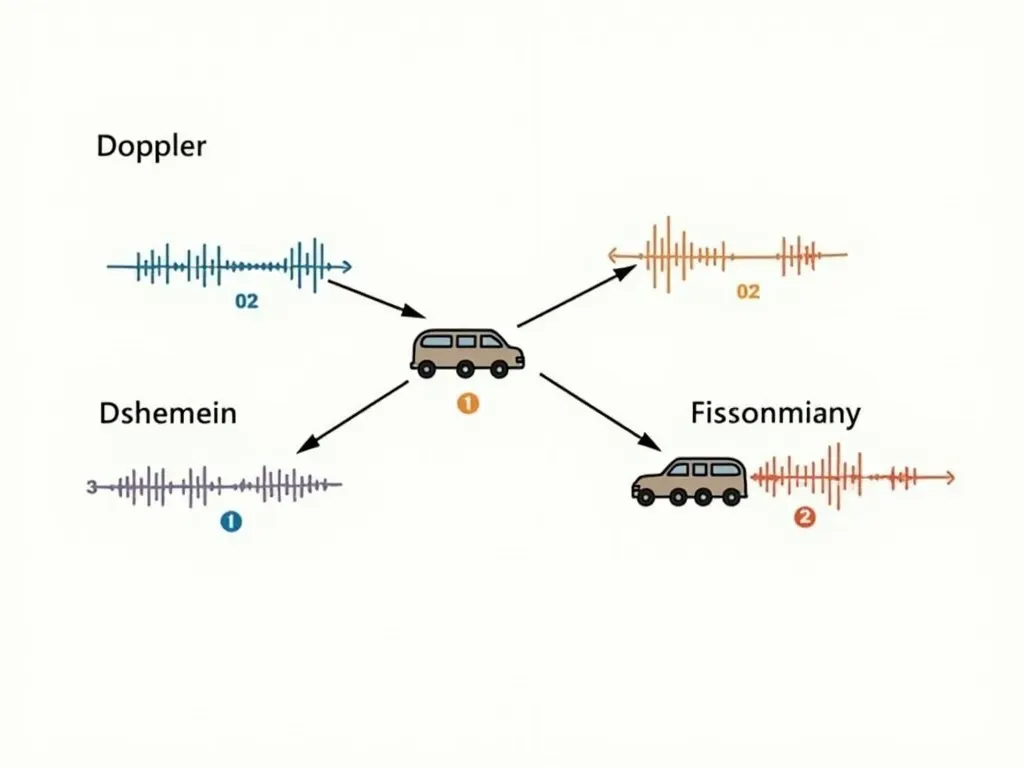
ドップラー効果とは、観測者が静止している場合に比べ、波源が動いているときに、観測される波の周波数が変化する現象を指します。救急車のサイレンを例に挙げれば、そのサイレンが近づくと音が高くなり、離れると音が低く聞こえる現象です。
「ドップラー効果は、目には見えないが、耳では確実に感じる!」
ドップラー効果の公式
ドップラー効果の公式は、次のように表されます。
周波数の一般的な式は次の通りです:
ここで:
f'= 観測者が受け取る周波数f= 波源から放出される周波数v= 波の速度(媒介物中の速度)v_r= 観測者の速度(波源に向かっている場合は正)v_s= 波源の速度(観測者に向かっている場合は正)
ドップラー効果の原理の導出
ドップラー効果の原理を理解するには、観測者と波源の相対的な動きに基づいています。バルセロナからサンパウロへ向かう電車の動きを想像してみてください。このように、電車が通過するとき、乗客は通過していく電車の速度に応じて音が高くなることを感じます。
式のコンセプトは、波長の変化と波の速度の変化に基づいています。具体的には、波源が移動すると、波が観測者に届くまでの距離が変わるため、時間あたりに受け取る波の数も変わります。
実生活での応用例
ドップラー効果は、交通の違反そのものから、天体物理学に至るまで、様々な分野で利用されています。
- 救急車のサイレン – 前述の通り、観測者に近づくと音が高く、去ると音が低くなります。
- 天文学 – 星の光の赤方偏移や青方偏移を用いて、宇宙の膨張や天体の運動を観測します。
たいへん重要なポイント
ドップラー効果は、観測者または波源の運動によって周波数が変化するという基本的な原則に基づいています。これを正しく理解することで、より複雑な物理的現象を分析するための基盤を築くことができます。
グラフで理解するドップラー効果
まとめ
ドップラー効果は物理学における重要な現象で、周波数の変化が実際の動きによってどのように影響を受けるかを示しています。他の物理的現象を理解するための出発点として、ドップラー効果を深く掘り下げていくことが、学びの大きな一歩です。
「もしあなたが 音 や 光 の波動を学びたければ、ドップラー効果を無視することはできません!」🚀🎵